Join Algorithm
本节课主要讲的是实现等值内连接(inner equijoin join)的实现方式。等值内连接指返回两张表满足等值关系的部分。
一般情况下将较小的表作为左表(left table),即外表(outer table),较小指的是 page 数量少。这里的 outer 指的是在 Nested Loop Join 中处于外层循环的表。Join 也有早物化和晚物化之分,早物化是指将外表中 tuple 的属性,内表中 tuple 的属性都拷贝到输出 tuple 中,这样上层的 operator 就不需要再到原始的表中去取数据了。晚物化就是只在新生成的 tuple 中保存原 tuple 的 record id。


假设表 R 大小为 M 个 page, 包含 m 个 tuple,表 S 大小为 N 个 page, 包含 n 个 tuple,以下内容都基于此假设。R⨝S 表示连接(join)操作,使用非常频繁,需要着重优化。R×S 表示笛卡尔积或交叉积(cross product),会产生包含 m * n 个 tuple 的输出表,使用 R×S 再加上 selection 虽然能达到 join 的目的,但是十分低效。
主要有三种实现 Join 的方式:
- Nested Loop Join 嵌套循环 Join 又有三种实现方式:
- Simple
- Block
- Index
- Sort-Merge Join
- Hash Join
Stupid Nested Loop Join
假设 buffer pool 中只有三个 page,一个作为左表输入,一个作为右表输入,一个用作输出。朴素的方法如下:对于从外表(左表)取出的每个 tuple,遍历一遍右表,找到匹配的 tuple 输出。**I/O 代价为 M + (m * N)**,前面的 M 是因为要从外表中取每个 tuple,所以需要读外表的 M 个 page,m * N 是因为对于外表中的每个 tuple,都需要完整地读一遍右表。因为太蠢了所以没人会用。

Block Nested Loop Join
还是考虑只有三个内存 page 的条件,但是可以处理得稍微聪明一些:以 block(page) 为单位,而不是 tuple 来处理关系。先从左表选取一个 page,从右表选取一个 page,再从这一对 page 内部选取 tuple 进行 join:
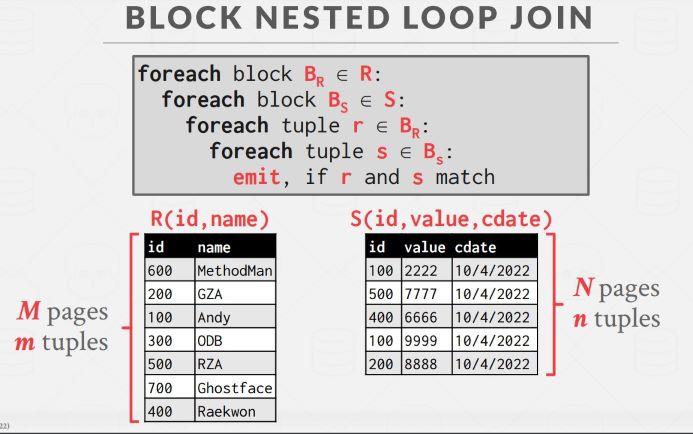
可以感受到其实面向磁盘的很多算法优化的出发点都是尽可能利用好已经缓冲在内存中的数据,在读下一个 page 进缓冲区之前,要对缓冲区中的数据作尽可能多的处理。比如 Stupid Nested Loop Join 之所以 stupid 是因为它会为左表中的区区一个 tuple 扫描整个右表,那么当要处理下一个 tuple 时,又要从右表的开始处,将上一步加载过的 page 再加载一遍,这就是没有利用好右表已缓冲的数据,Block Nested Loop Join 好在对于右表已缓冲的一个 page,它会与左表一个 page 的数据进行 join 后,再移动到右表的下一个 page,这样尽可能利用了右表的缓冲 page。
Block Nested Loop Join 的 I/O 代价为 M + (M * N)。此外要将小的表作外表,表的大小是指占用 page 的多少,而不是包含 tuple 的多少,因为从 I/O 代价公式可以看出 I/O 代价是与 page 数量而不是 tuple 数量有关的。
如果我们有不止三个 buffer pool page,那还可以进一步优化。假设 buffer pool 容量为 B,可以每次读取外表的 B - 2 个 page,另外两个给内表和输出。此时 I/O 代价为 M + (M / (B-2) * N) :
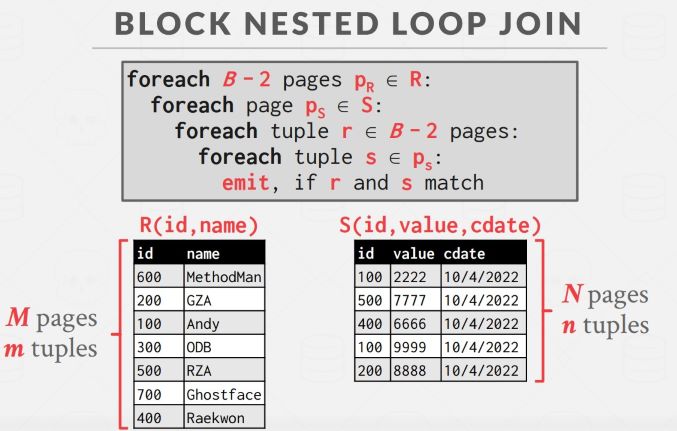
Index Nested Loop Join
如果对应属性上有索引的话就更方便了,可以直接遍历内表的索引而不是内表本身。这里假设通过索引查找一个 tuple 的代价是常数 C,则 **I/O 代价为 M + (m * C)**:

Sort Merge Join
分为两个阶段:
- 排序:对要连接的两个表分别排序,可以使用外部排序算法,见lecture10笔记。
- 合并:对两个已排序的表建立 cursor,检查两个 cursor 所指记录是否匹配,匹配就输出,否则像归并算法那样移动 cursor
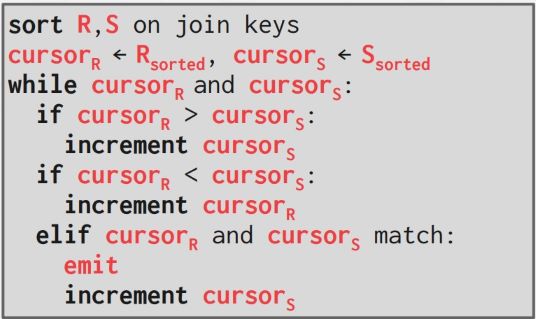
不过这种方法有可能内表出现回溯,比如下面的情况,当两个 cursor 相等时,按照算法递增内表 cursor,然而外表下一条记录的 key 是重复的,这时内表需要回溯:




所以还需要跟踪每个相同 key 值的起始位置,便于回溯的时候定位起始点。在不考虑回溯情况下,I/O 代价如下,即两个表的排序代价加上从头到尾遍历两个表的代价:

Hash Join
Hash Join 的基本思想是在 join 属性上具有相同值的记录一定会 hash 到相同的分区中,可以大大减少要比较的数据范围,只需要相同分区内的数据进行 join 就好了,因为 join 属性相同的记录不可能分到不同的分区(当然 join 属性不同的也可能分到一个分区,所以在 join 的时候也需要比较 join key 本身是否相等)。
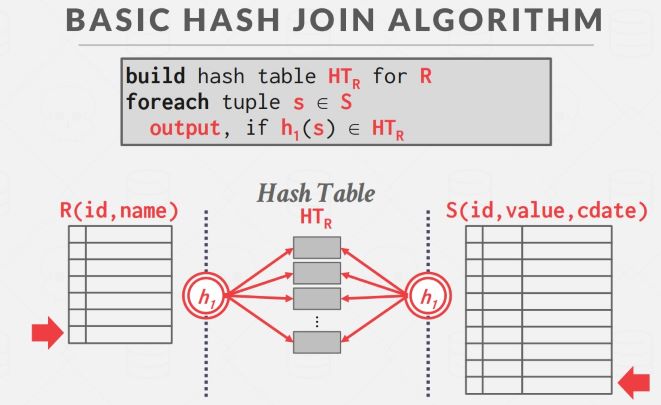
Basic Hash Join
分为两个阶段:
- Build:使用哈希函数 h1 为外表建立一个哈希表,可以使用任何种类的哈希表实现,一般来说线性探测法在实践中性能最好
- Probe:遍历内表,对每个元组使用 h1 计算其所属分区,到对应分区内去寻找匹配的 tuple
这个 cost 计算暂时不是很理解,先放这里等以后再看:

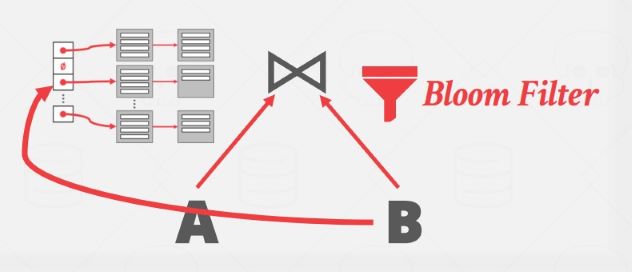
有一种优化措施是在 build 哈希表的时候也构建一个 bloom filter,在 probe 阶段先查询 bloom filter,可以避免许多对哈希表的不必要访问。
Partitioned Hash Join
如果内存不足以为整个外表建立哈希表怎么办呢?就又要使用面向磁盘数据库常用的策略了——分治。像 External Merge Sort 和 External Hashing Aggregate 都有分治思想。先用哈希函数 h1 将外表和内表的数据根据 join 属性在磁盘上分区:
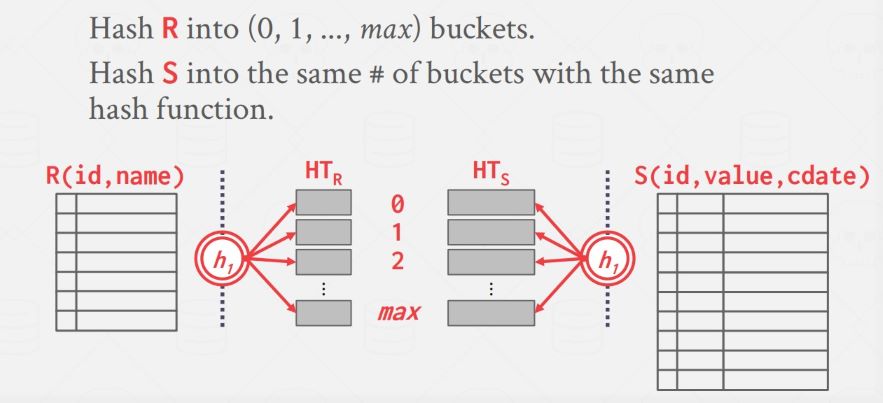
此时可以肯定的是两个表中 join 属性具有相同值的记录一定处于同层的两个分区中,所以只需要每次对同一层的两个分区进行 basic hash join 就可以了,因为经过了分区,每个 bucket 中的数据量大多数情况下都可以放入内存了。
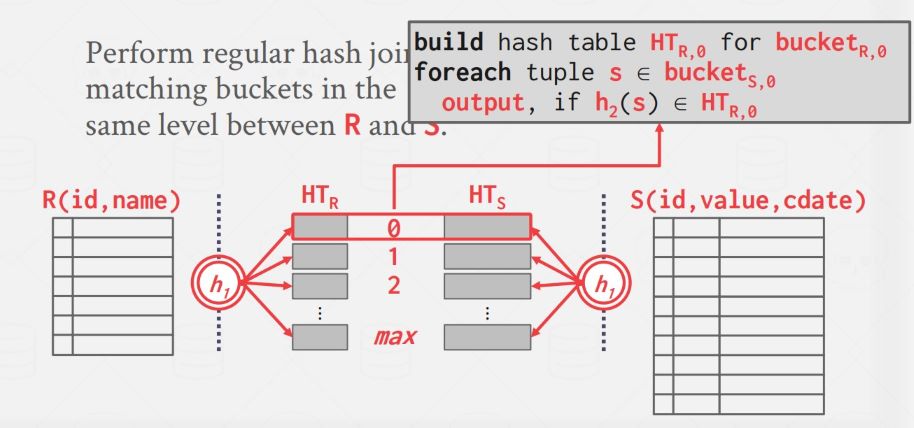
Recursive Hash Join
如果情况再极端一点,比如表中数据量非常大,或者外表中 join 属性值相同的记录非常多,导致某个 bucket 过大而无法放入内存,这时可以对这个 bucket 故技重施,使用另一个不同于 h1 的哈希函数 h2 将这个 bucket 二次分区,这就是递归 Hash Join:
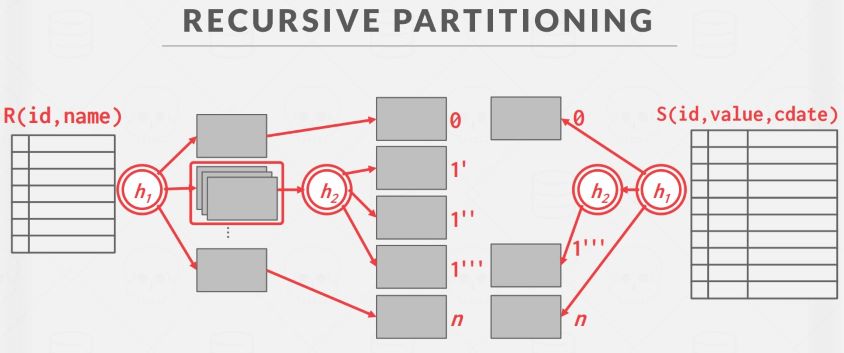
I/O cost 如下:
