cmu15445-lecture10笔记

cmu15445

Sorting & Aggregation Algorithms

执行计划 (query plan)

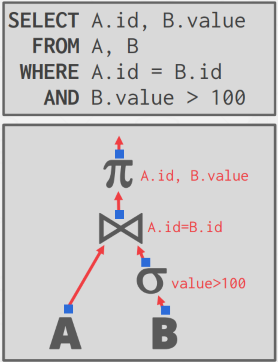
一条 SQL 查询语句首先被解析成抽象语法树，接着构建出对应的执行计划树(query plan tree)或 DAG。一个执行计划树的叶子节点对应底层的数据访问接口(access method)，包括通过索引查询或者直接扫描 table 本身等。叶节点将获取的数据传递给上层的节点(operator)，每个 operator 对数据进行处理后继续向上传递，直到根节点，将最终结果返回给查询者。数据库系统需要根据一条 SQL 语句，生成最优的执行计划，因为 SQL 只是表明了“我想要满足何种条件的数据”，而数据库要找到最优的执行方式。优化方式大体分为两种：一是选择合适的算法，二是对 query plan 进行重构，比如将 select operator 排在 join operator 之前(谓词下推)

p1

此外，对于面向磁盘的数据库来说，我们不能假设查询结果能够完全放入内存中，需要借助 buffer pool 来保存中间结果。所以衡量一个算法优劣的主要标准不再是以往的时间复杂度，而是 IO 的频次。一个时间复杂度较高，但大多数是 sequential I/O 的算法要优于另一个时间复杂度较低，但多数是 random I/O 的算法。

排序(Sorting)

关系模型中数据是无序的，然而有不同的场景需要进行排序

  • 用户指明需要有序的结果(通过 order by)
  • 数据库内部将数据排序便于处理，比如去重(distinct)，将有序的元组 bulk loading 进 B+ 树效率更高、支持聚合等。

如果数据可以全部塞进内存，那么直接用标准的快排之类的算法就好了，否则就需要考虑磁盘 I/O 的代价，普通的内存排序算法带来的 random I/O 是无法接受的。

Top-N heap sort

当遇到 order by + limit N 的查询时，数据库不需要将所有数据全部排序。此时最好的情况是当内存装得下 N 个元素时，可以在内存维护一个有序的优先队列(课件里是这么写的，感觉这里的 heap 不是传统的堆的定义，标准的堆只要求根节点大于左右子树，不要求全局有序，这里是全局有序的)。当新插入元素大于队头时，就插入到队头位置，否则插入到其应处的位置，队列满时队尾出队。当所有数据都插入一遍以后，留在队列中的即为 top N。

p1

External Merge Sort

sorted runs 的概念：

一个 sorted run(归并段) 就是一个有序的 key/value pair 的列表。突然想到 leveldb 中也有 sorted run 这个概念，看来是一个外部归并排序中的专用概念了。这里的 key 很简单，就是要排序的属性(列)，value 有两种选择：一是保存整个 tuple 的内容(早物化)，一种是只保存对应 tuple 的 record id，直到最后一刻才去磁盘取对应的内容(晚物化)。前者优点是，当要返回数据给客户端时， tuple 的内容已经在内存中了，不用再去磁盘中取，缺点是在排序过程中，可能要将一个 tuple 内容从一个 sorted run 拷贝到另一个 sorted run，导致某一时刻一个 tuple 的内容存在多个副本。后者优点是几乎没有拷贝的开销，但是最终还是要去磁盘取 tuple，列数据库中用的比较多。另外早物化可以通过提前进行 project，只在 value 中保留需要的数据。

p1

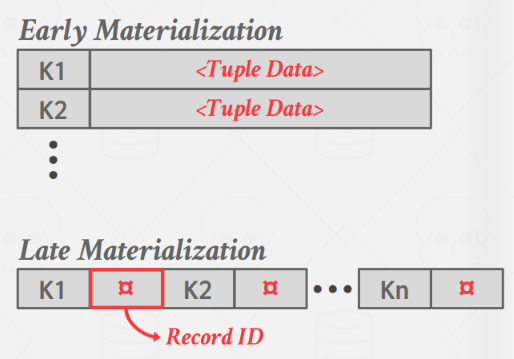
外部归并排序的思想是将所有要排序的数据分成多个 runs，分别对其排序，形成多个 sorted runs，即归并段，然后经过多轮合并，将小归并段合成大归并段。整个过程可以总结成两个阶段：

  • 排序阶段：该阶段负责创建归并段，每个归并段包含全体数据的一部分，并且归并段内部是排好序的
  • 合并阶段：归并段进行合并，生成更大的归并段

2-Way External Merge Sort

2路归并是指在合并阶段的每一轮中将2个归并段合并。设数据总共有 N page 大小，buffer pool 的容量是 B 个 page。在排序阶段(pass 0)中，将每个 page 读入 buffer pool，排好序后输出，这样创建出 N 个 1 page 大小的归并段：

p1

接下来在合并阶段的每一轮(pass)中，选取2个归并段作为输入，用归并算法合成一个更大的归并段。所以2路归并只需要B >= 3 即可(每一轮归并中2个 page 用作输入，1个 page 用作输出)。注意，无论输入的归并段大小有多大，一个归并段只需要1个 buffer pool 中的 page，因为归并算法中2个归并段中的 cursor 是只需要正向移动，不会回溯的，当处理完一个归并段中的1个 page，只需要清空 buffer pool 的这个 page，读入该归并段中的下一个 page 即可。同理，不论输出段有多大，也只需要1个 buffer pool page，当其写满以后溢出(spill)到磁盘就可以清空以写下一个 page 的内容了。

p1

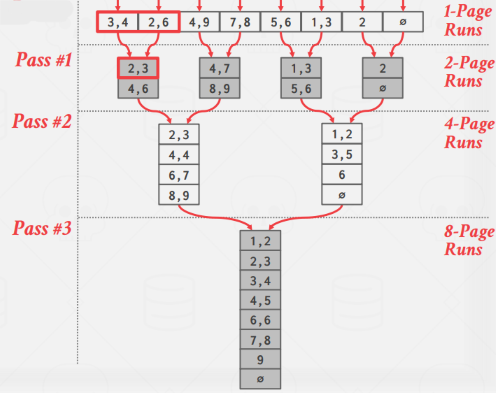
每一轮合并中归并段个数变为上一轮的 1/2，归并段大小变为上一轮的2倍，所以有如下公式：

  • 需要的总轮数(趟数) # of passes = 1 + ⌈ log2N ⌉ (1 轮用于生成归并段，⌈ log2N ⌉ 轮用于合并)
  • total I/O cost = 2N * (# of passes) (每一轮中，对于每个 page，都需要一次读入和一次写出)

2路归并的局限在于即使有多于 3 个的 buffer pool page，也无法很好地利用。

General External Merge Sort

k路归并是2路归并的扩展，这部分感觉教材 15.4.1 节讲得更清楚一些。设数据总共有 N page 大小，buffer pool 的容量是 B 个 page。在排序阶段，一次读入 B 个 page，排序，输出为一个归并段，循环直到处理完所有数据：

1
2
3
4
5
6
7
i = 0
repeat
	读入关系的B个块或关系的剩余部分，以较小者为准，
	在内存中对这B个块的数据排序，
	将排好序的数据写到归并段文件Ri中
	i = i + 1
until 到达文件末尾

这样会产生 M = ⌈ N / B ⌉ 个归并段，每个归并段大小为 B 个 page (最后一个可能不足 B)。在合并阶段，每一轮可以合并 (B - 1) 个段(为每个段分配一个输入 page，还预留一个作为输出 page)。现在假定 M <= B - 1，过程如下：

1
2
3
4
5
6
7
从M个归并段文件Ri各读入一个块到 buffer pool 中:
repeat
	从所有缓冲块中按序取第一个tuple;
	将该tuple写到输出中，并将其从缓冲块中删除;
	if 任何一个归并段Ri的输入缓冲块为空 and not 到达Ri末尾
		then 读Ri的下一块进缓冲块
until 所有输入缓冲块均为空

如果第一阶段产生的归并段个数 M > B - 1，意味着没法同时为每个段分配一个 buffer pool page，这时候需要分多趟，每趟依然合并 B - 1 个段。

  • 需要的总轮数(趟数) # of passes = 1 + ⌈ logB-1 ⌈ N / B ⌉ ⌉
  • total I/O cost = 2N * (# of passes)

使用 B+ Tree index 帮助排序

有时如果要排序的属性上已经建立了索引，那么可以考虑直接遍历索引。如果是聚集索引，也就是 B+ Tree 索引中的逻辑顺序和 page 在磁盘上的物理顺序相同，直接遍历索引是很方便的，因为相当于顺序 I/O：

p1

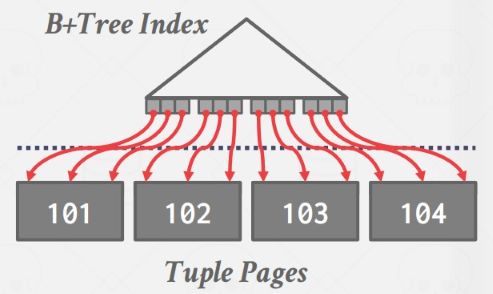
如果是非聚集索引，遍历索引就糟糕透顶了，因为要跟随 B+ Tree 叶节点中的 record id 去找对应的 page，而这些 page 物理顺序和B+ Tree 叶节点顺序不同，相当于 random I/O 了：

p1

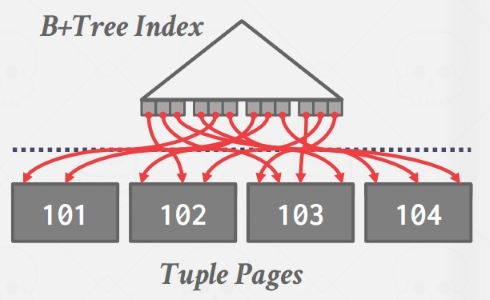
聚合(Aggregations)

通常有2种实现选择：

  • Sorting
  • Hashing

Sorting

Sorting 是很直接的方法，比如下面的例子，将对应列排序，然后从头到尾扫描一遍，遇到与上一个 key 重复的就剔除掉：

p1

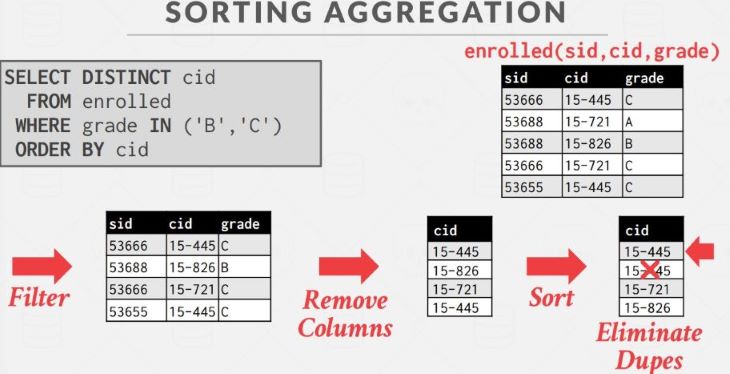
但是如果没有指定 order by，只希望去重，那这里的排序工作就显得冗余了，可以考虑 Hashing

Hashing Aggregations

最简单的方式就是在内存中维护一个临时的 Hash Table，遍历所有数据，对于每条 record，到 Hash Table 中查看其是否存在，根据不同的聚合类型进行不同的操作，比如是 DISTINCT 就抛弃重复的，是 GROUP BY 就执行对应的聚合计算。问题在于当所有数据不能全塞进内存的时候怎么办。

External Hashing Aggregate

基本思想是分两个阶段：

  • 阶段一：将全量的数据根据要 GROUP BY 的属性在磁盘上进行分区(partition)
  • 阶段二：将各个分区依次调入内存，将分区中的数据插入一个内存 Hash Table 中，如果 Hash Table 满了，就将其丢弃并创建一个新的即可。

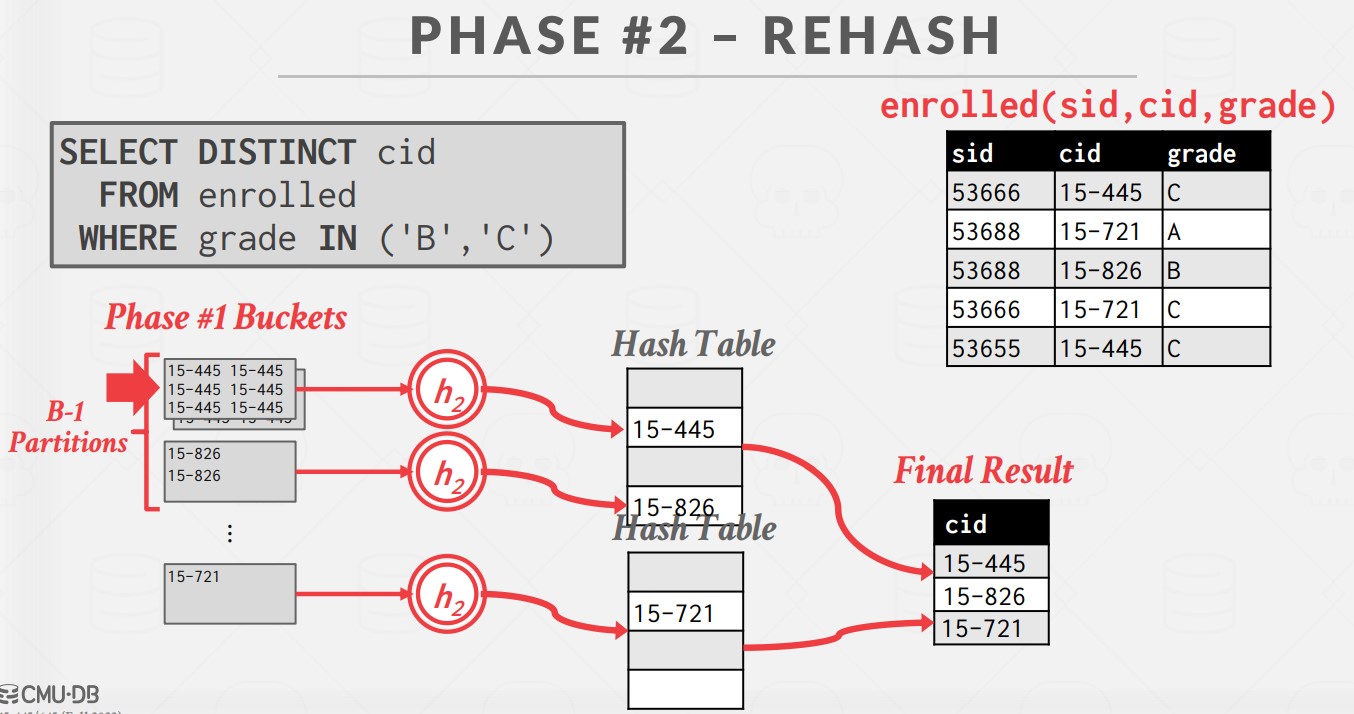
阶段一如下：使用哈希函数 h1，根据目标的 hash key 将 tuple 分割到磁盘中的不同分区，使得所有匹配的 tuple 放在同一个分区中。一个 partition 应该是能够全部放入内存缓冲区的，当缓冲区满会将分区溢出(spill)到磁盘上。

p1

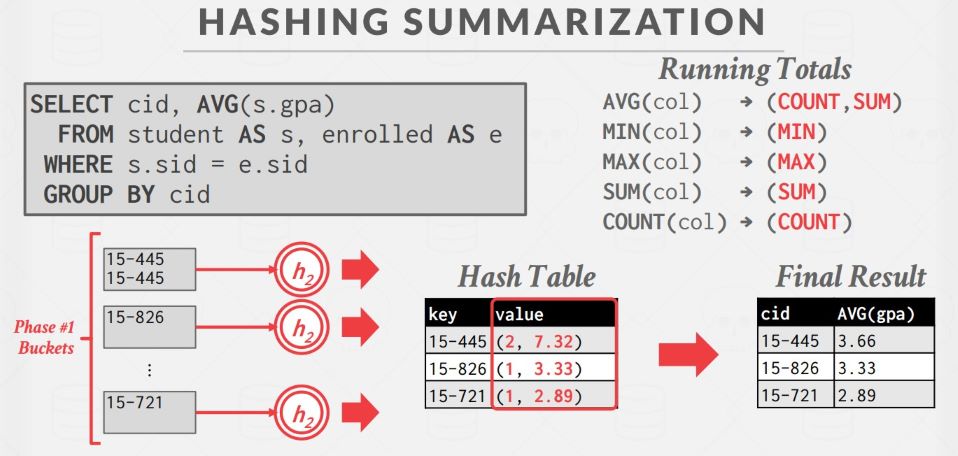
阶段二如下：对磁盘上每个 partition，将其读入内存，使用第二个哈希函数h2，建立一个内存 Hash Table，把匹配的 tuple 聚合在一起。此外，Hash Table 中可以保存 GroupByKey -> RunningValue 的配对，以计算聚合。RunningValue的内容取决于聚合函数。当向 Hash Table 中插入一个新 tuple 时，如果 Hash Table 中已有对应的 GroupByKey，那么就使用聚合函数更新 RunningValue，否则就插入一个新的 GroupByKey→RunningValue 对。

p1

p1