对于补码和反码本质的理解

2023-10-10

最近复习 408 的时候对补码和反码的本质有了新的理解，整理记录一下。或许有错误或者不严谨之处，留给日后修正。下面是一些对补码和反码新的认知：

补码和反码在计算机看来，根本没有符号位这个概念，换句话说从计算机的视角看，补码和反码都是正数。
补码和反码能够出现，有一个大前提，就是今天的计算机所使用的计量系统是基于模运算的，具体表现就是使用有限的二进制位数去表示一个数，所以每一个加减运算都有一个隐式的取模操作。对于补码来说就是丢弃最高位的进位，对于反码就稍微复杂一些，具体下面再说。
反码的本质和补码相同，它们只是基于不同的模，可以说反码是有缺陷的补码(体现在 0 有两种编码，以及取模操作的不便上)。

关于补数

众所周知计算机只能作加法，补码和反码都是一种补码，它们都是使用补数的概念来将减法变成加法。对于补数我的理解是若 a + b = m, 则 a 和 b 互为补数，m 为这个计数系统的模。此时 (x - a) % m = (x + b) % m，即在模m的情况下，减去一个数等于加上它的补数。举个例子，钟表就是以 12 为模的计数系统。现在时针指向 8 点，要让它指向 7 有两种选择：

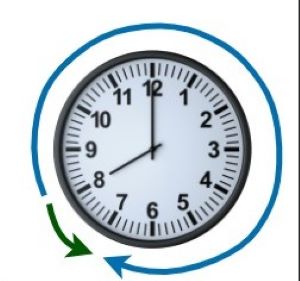
逆时针旋转 1，即 8 - 1 = 7
顺时针旋转 11，即 (8 + 11) % 12 = 7，这里 11 即为 1 在模为 12 的计数系统下的补数。

所以在钟表这个计数系统中，可以用 11 表示 -1。推广一下，在以 m 为模的计数系统里，要想消除负数或者说减法这个概念，可以将负数 x 用它绝对值的补数表示，即 [x]_补 = m - |x| 或 [x]_补 = m + x。[x]_补就是所谓的补码了。于是我们得到了一个只用顺时针旋转就能实现加减的钟表，这不正是计算机需要的吗。

补数和同余定理

使用补码来表示负数的正确性来源于同余定理的支持。先补充一下同余定理：设 m 是大于1的正整数，a、b 是整数，如果 m | (a - b)，则称 a 与 b 关于模 m 同余，记作 a ≡ b (mod m)

同余性质：

反身性：a ≡ a (mod m)
对称性：若a ≡ b (mod m)，则b ≡ a (mod m)
传递性：若a ≡ b (mod m)，b ≡ c (mod m)，则a ≡ c (mod m)
同余式相加：若a ≡ b (mod m)，c ≡ d (mod m)，则 a ± c ≡ b ± d (mod m)
同余式相乘：若a ≡ b (mod m)，c ≡ d (mod m)，则 ac ≡ bd (mod m)

设 a < 0，b 为 a 在以 m 为模的系统下的补码，即 b 是 |a| 的补数。

可得 |a| + b = m
因为 a < 0, 所以 b - a = m，由同余定理得 a ≡ b (mod m)
由同余性质 1，3 可得 (x + a) % m = (x + b) % m
即加上一个负数等价于加上它的补码

可见求一个负数的补码，等价于求它绝对值的补数，等价与求它的同余。

将补码应用于计算机

计算机领域里的补码 (2 的补码) 使用的是以 2ⁿ 为模的系统，反码 (1 的补码) 使用的是以 2ⁿ - 1 为模的系统。这里 n 是数据的位数 (不区分符号位数值位，因为根本没有符号位这个东西)。引用 CSAPP 里的一段旁注：补码英语里是 Two’s complement，反码是 Ones’ complement，这里 2 是单数 1 是复数，原因是补码使用的模是 2ⁿ，只有一个 2，反码使用的模是 2ⁿ - 1，是 [11…111] 共 n 个 1。所以感觉将补码翻译成 “对 2 求补”，反码翻译成 “对 1 求补” 更贴切一些。

因此 2 的补码对负数 x 的定义是 [x]_补 = 2ⁿ + x， 1 的补码对负数 x 的定义是 [x]_反 = 2ⁿ - 1 + x。这也是为什么可以用反码加 1 来得到补码。

由于使用 2 补码的系统在加减运算时将最高位进位直接丢弃，这就相当于对 2ⁿ 进行了一次取模操作，只不过是隐式的 (使用 1 的补码就会带来问题，下面再说)。至于为什么补码的符号位可以参与运算，个人认为这是个伪命题，因为二进制数本身没有正负，或者说都是正的，没有符号位数值位之分。例如 4 位的补码如图：

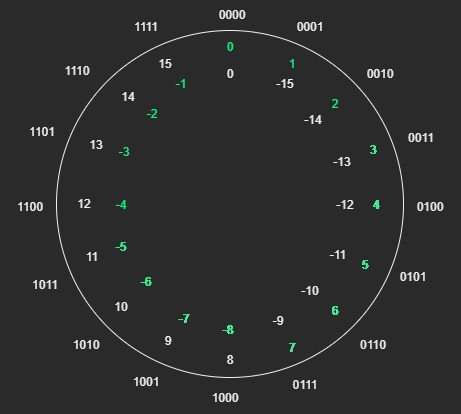
计算机只能作加法，所以计算机对这些数只是执行简单的二进制加法而已，但是因为有模的存在，可以表现为在数轴上的回退。从补码的原理角度看，每个二进制数都有两个含义：+x 或 -(m - x)。如本例，对任意一个数执行二进制加法，可以理解成增加 x，也可以理解成减少 16 - x，反正对于计算机来说是等价的。所以每个二进制数都可以表示一个正数或负数，只是我们人为规定，最高位为 0 的二进制数，使用它的正数含义，最高位为 1 的数，使用它的负数含义。即选取图中绿色的数作为当前这个计数系统的表示范围。于是人们将最高位定为符号位，它只是一个人为的划分标志而已，本身就是数值的一部分。

为什么反码存在缺陷

反码以 2ⁿ - 1 作为模，那么 0(二进制全 0) 和 2ⁿ - 1 (二进制全 1) 这两个数互为补数，都表示 0，浪费了一个编码，使得计数系统容量变成了 2ⁿ - 1。更重要的是，反码的取模没法像补码那样直接舍弃高位，因为那相当于模 2ⁿ，而反码是以 2ⁿ - 1 为模的，所以当反码最高位出现进位时，需要将进位加到低位上。例如 3 - 2 = 0011 + 1101 = 0000 + 1 = 0001。我是这样想的，因为模的是 2ⁿ - 1，所以当达到全 1 的时候就该归零了，下一次就要从 1 开始了，然而下次加 1 导致了进位，相当于这个加 1 被进位消耗掉了，所以需要在低位 + 1 修正。或者更直观的想法如图：

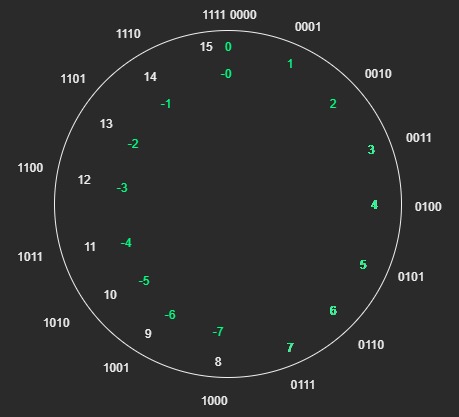
当计算 a - b 时，相当于顺时针移动 2ⁿ - 1 - b (即 b 在以 2ⁿ - 1 为模的系统中的补数) 个单位，最高位出现进位说明越过了顶端的 1111，而由于 0000 也表示 0，所以越过顶端时有一步移动是无效的(从 -0 移到 +0)，所以需要再补偿一步进行修正。大概是因为这些缺陷导致反码没有广泛使用，但 ip，udp 报文的校验和用的是反码，好像是可以做到屏蔽大小端的差异，没有深究，它的计算过程中也需要进位回卷，我猜想是因为上述的原因。

参考链接

https://blog.csdn.net/qq_45472866/article/details/114779170

https://blog.csdn.net/wu_nan_nan/article/details/54633506

https://www.zhihu.com/question/20458542/answer/40759880

https://www.cnblogs.com/codetravel/p/4361345.html